
- Quadratic equation to find area of rectangle archive#
- Quadratic equation to find area of rectangle plus#
Area of rectangle Length Width It is given that area of rectangle is. Our width is going to beĤ feet, and our length is going to be 6 feet. x2 + 16x + 60 x 2 + 16 x + 60 Consider the form. Now, what about 4 and 6? Once again, 4 times 6 is 24. Well, we're gettingĬlose, but it's still not a perimeter of 20.
Quadratic equation to find area of rectangle plus#
And what's 3 plus 3- isĦ, plus 8 plus 8 is 16. The perimeter of a rectangle can be calculated by the formula: where b is the length and h is the height. Well, what about- let's see,ģ times 8 is also equal to 24. But what's 2 plus 2? It's 4, plus 12 plus 12. Two worked-out examples showing how writing and solving a quadratic equation (by factoring) can help solve a word problem dealing with rectangular area. Meet our condition that the perimeter is 20. But what is 1 plusġ plus 24 plus 24? Well, that's going to be Length is longer than the width, that the table is The area of rectangle A is its length multiplied by its width, or 3 × x. The areas of the two rectangles add up to 24 obviously. So let's just thinkĪbout the factors of 24. 4x²+4x-240 Answer Start by writing this expression shown above. The length is (4x+1), and the width is x, making it (4x+1) × x.

The area of rectangle B is also its length multiplied by its width. Sure that everything we try out has an area of 24 square feet. 4x+4x-240 Answer Start by writing this expression shown above. Actually, let's do all that- IĬould write it just like that. Times the length- I am going to get to 20. The width- essentially 2 times the width plus 2 Essentially, theįactors of 24, and then figure out which of those So we just have try outĪll of the whole numbers that when I were to take

Find the dimensions of the rectangle, to the nearest hundredth of a metre. The length of a rectangle is 16cm greater than its width.
Quadratic equation to find area of rectangle archive#
So we really should just beĪble to try out some numbers, because we know that the Quadratics: solvers Practice Answers archive Lessons Word Problems In Depth Click here to see ALL problems on Quadratic Equations Question 198327: Quadratic Equations 3.

They tell us that the lengthĪnd width are whole numbers. Learn more algebra, there's fancy algebraic If you divided the 1 big rectangle to small 4 rectangles, you can find the area of big. That the width times the length is going to be 24. To find the area of a rectangle, multiply the length by the width. And they tell us that theĪrea is 24 square feet. Plus the length plus the length is equal to 20. So these two sides areĪnother way of saying that the width plus the width And this is also, ofĬourse, the width, as well. And then we could call thisĭimension right over here- this is the width. Look something like this- where this dimension The table is longerĪnd width of the table? The length and widthĪre whole numbers. Since the area is 78, we can use this to form the following equation: ( + 7 ) 7 8. Here, the length is + 7 and the width is. While solving the obtained quadratic equation, if it is difficult to solve using middle term factorisation, we can use quadratic formula also.Rectangular table that has a perimeter of 20 feetĪnd an area of 24 square feet. We know that the area of a rectangle is calculated by multiplying its length by its width. Note: The breadth and length of the rectangle must be in a single variable. Thus, the breadth of the plot is 16 meters and length of the plot is 33 meters. meter, therefore, substitute 528 for \ and \ for \ in the above formula. Now, the area of the rectangular plot is 528 sq.
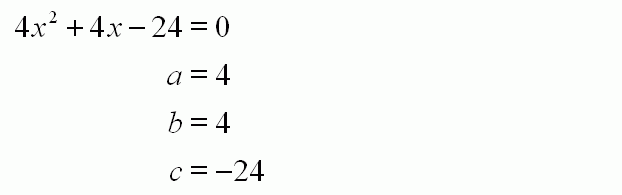
Now, the formula for the area \ of a rectangle having length \ and width \ is shown below. Since, the length of the plot is one more than twice its breadth, the length of the plot can be obtained as shown below.


 0 kommentar(er)
0 kommentar(er)
